Die Sterbetafel

Die Sterbetafel ist eine Ausscheideordnung, die darstellt, wie sich ein fiktives Kollektiv von Personen aus einer bestimmten Personengruppe durch Tod erwartungsgemäß verringert.


John Graunt – Titelblatt seines Buchs Natural and Political Observations Made upon the Bills of Mortality (1662)


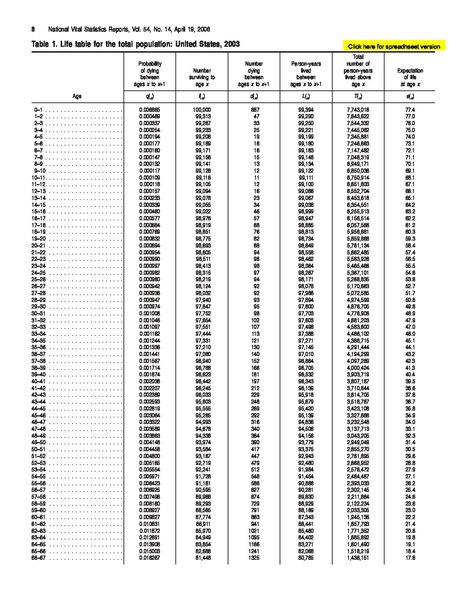
Sterbetafel

Geschichte

Sterbetafeln gab es bereits in der frühen Neuzeit. Sie gehen auf John Graunt zurück, der im Jahre 1662 die Sterbeverzeichnisse in London analysierte, hieraus die erste Sterbetafel berechnete und damit erstmals für jedes Alter Überlebenswahrscheinlichkeiten angab. Diese Daten veröffentlichte er in seinem Buch Natural and Political Observations Made upon the Bills of Mortality (1662).
Elemente einer Sterbetafel

In der Sterbetafel werden getrennt nach Geschlecht meist folgende Werte für die Alter x = 0 {\displaystyle x=0} x=0 bis zum Endalter (meist 100 oder höher) aufgeführt:

die alters- und geschlechtsabhängigen Sterbewahrscheinlichkeiten der betreffenden Personengruppe q x {\displaystyle q_{x}} q_{x},
daraus errechnet die Anzahl l x {\displaystyle l_{x}} l_x der jeweils bis zum Alter x {\displaystyle x} x Überlebenden eines fiktiven Kollektivs in der Personengruppe und
die pro Altersjahr x {\displaystyle x} x Gestorbenen d x {\displaystyle d_{x}} d_{x} des fiktiven Kollektivs.

Die Überlebenswahrscheinlichkeit p x {\displaystyle p_{x}} p_{x} sagt für jedes erreichte Lebensalter x {\displaystyle x} x aus, mit welcher Wahrscheinlichkeit ein Individuum des Kollektivs das Alter x + 1 {\displaystyle x+1} x+1 erreicht. Die Wahrscheinlichkeit einer x {\displaystyle x} x-jährigen Person, vor Erreichen des Alters x + 1 {\displaystyle x+1} x+1 zu sterben, also die Sterbewahrscheinlichkeit q x {\displaystyle q_{x}} q_{x}, ist damit 1 − p x {\displaystyle 1-p_{x}} 1-p_{x}.

Häufig werden für Männer und Frauen getrennte Sterbetafeln verwendet. Aus der Sterbetafel lassen sich die Lebenserwartung eines neugeborenen Kindes und die sog. fernere Lebenserwartung, also die Lebenserwartung einer Person im Alter x {\displaystyle x} x, errechnen. In der Schreibweise der Versicherungsmathematik wird das Alter von Männern mit x {\displaystyle x} x, das von Frauen mit y {\displaystyle y} y bezeichnet. Die Sterblichkeit eines x {\displaystyle x} x-jährigen Mannes wird mit q x {\displaystyle q_{x}} q_{x}, die einer y {\displaystyle y} y-jährigen Frau mit q y {\displaystyle q_{y}} q_{y} notiert.

Neben den Sterbewahrscheinlichkeiten q x {\displaystyle q_{x}} q_{x} werden für jedes Alter x {\displaystyle x} x in der Sterbetafel die Anzahl l x {\displaystyle l_{x}} l_x der noch lebenden und die Anzahl der im Alter x {\displaystyle x} x versterbenden Personen d x {\displaystyle d_{x}} d_{x} tabelliert. Dabei geht man oft von l 0 = 100.000 {\displaystyle l_{0}=100.000} l_{0}=100.000 oder l 0 = 1.000.000 {\displaystyle l_{0}=1.000.000} l_{0}=1.000.000 neugeborenen Personen aus. Damit kann man anschaulich darstellen, wie sich ein Personenkollektiv im Modell durch die Sterbefälle reduziert. Es gilt:

l x = l x − 1 ⋅ ( 1 − q x − 1 ) {\displaystyle l_{x}=l_{x-1}\cdot (1-q_{x-1})} l_{x}=l_{{x-1}}\cdot (1-q_{{x-1}})

d x = l x − l x + 1 = l x ⋅ q x {\displaystyle d_{x}=l_{x}-l_{x+1}=l_{x}\cdot q_{x}} d_{x}=l_{x}-l_{{x+1}}=l_{x}\cdot q_{x}

Das Endalter der Sterbetafel wird in der Regel mit dem griechischen Buchstaben ω {\displaystyle \omega } \omega bezeichnet (z. B. DAV 2008 T: ω = 120 {\displaystyle \omega =120} \omega =120; DAV 2004 R: ω = 120 {\displaystyle \omega =120} \omega =120, durch die Altersverschiebung kann das Endalter der DAV 2004 R Tafel allerdings deutlich größer werden).
Arten von Sterbetafeln

In der Versicherungswirtschaft werden vielfach Periodensterbetafeln eingesetzt. Dabei werden altersspezifische Sterblichkeiten von gleichzeitig lebenden Personen ermittelt. Periodentafeln beschreiben daher modellhaft die Sterblichkeitsverhältnisse gleichzeitig lebender Generationen innerhalb eines relativ kurzen Beobachtungszeitraums.

Im Gegensatz dazu sind Kohortensterbetafeln, die das Absterben eines Geburtsjahrganges beschreiben, aufgrund des langen Beobachtungszeitraums ungeeignet für die Kalkulation von Rentenversicherungen.

Unter einer Generationensterbetafel versteht man eine Sterbetafel, bei der die Sterblichkeit nicht nur vom Alter (und eventuell vom Geschlecht), sondern zusätzlich vom Geburtsjahrgang abhängt. Hierdurch lässt sich die steigende Lebenserwartung für später geborene Personen berücksichtigen. Generationentafeln liegen daher der Kalkulation von Rentenversicherungen zugrunde.[1] Die oben bereits erwähnten Tafeln DAV 1994 R und DAV 2004 R sind Generationentafeln. Manchmal wird die Geburtsjahrabhängigkeit vereinfachend dadurch abgebildet, dass später geborene Jahrgänge für die Kalkulation durch eine einfache Altersverschiebung „jünger gemacht“ werden.

Zum Teil werden auch Versichertensterbetafeln eingesetzt. Diese berücksichtigen, dass die Sterblichkeit des Versichertenkollektivs von derjenigen der Bevölkerung z. B. aufgrund einer Gesundheitsprüfung oder der Selbstselektion abweicht.

Die Methode der Sterbetafelberechnung gehört zu den nichtparametrischen Verfahren der Ereignisanalyse (event analysis).

Anwendung


Grafische Darstellung der Sterbetafel 2008/10 des Bundesamtes für Statistik

Wird die Tafel zur Kalkulation von Beiträgen eines Versicherungsvertrages oder der Deckungsrückstellung verwendet, so werden die Sterbewahrscheinlichkeiten erster Ordnung angesetzt. Sie sind gegenüber den Wahrscheinlichkeiten zweiter Ordnung (den "realistischen" Werten) mit Sicherheitsmargen versehen, um jeweils das Risiko vorsichtig einzuschätzen. Sie bilden geeignete Rechnungsgrundlagen. Entsprechende Sterbetafeln werden beispielsweise von der Deutschen Aktuarvereinigung e.V. (DAV) herausgegeben.

Besteht das Risiko im Tod des Versicherten (Lebensversicherungen auf den Todes- und Erlebensfall, Risikolebensversicherung), so werden die Sterbewahrscheinlichkeiten erhöht (Zuschlag). Ein Beispiel ist die Tafel DAV 2008 T.
Besteht das Risiko im Überleben (Rentenversicherungen), so werden die Sterbewahrscheinlichkeiten gesenkt (Abschlag). Ein Beispiel ist die Tafel DAV 2004 R.

Passende DAV-Tafeln dürfen für die Berechnung der in der Bilanz einer Versicherung auszuweisenden Deckungsrückstellung verwendet werden. Die Tafel DAV 1994 R berücksichtigt den Trend zur größeren Lebensdauer (wegen des medizinischen Fortschritts und der Verbesserung der Lebensumstände) für später geborene Personen aus heutiger Sicht nicht ausreichend vorsichtig, und darf daher nicht mehr von Rentenversicherungen verwendet werden.

Die zur Kalkulation von Altersrenten verwendeten Sterbetafeln (Rententafeln) berücksichtigen die steigende Lebenserwartung. Die anzusetzende Sterbewahrscheinlichkeit hängt damit nicht nur vom Alter x {\displaystyle x} x, sondern auch vom Geburtsjahrgang ab, da seit Jahrzehnten von Geburtsjahrgang zu Geburtsjahrgang die Lebenserwartung zunimmt. Die damit entstehende zweidimensionale Tafel mit einer Altersverschiebung wird auch zu einer eindimensionalen Tafel vereinfacht.

Siehe auch

Demografie
Lebenserwartung
Heubeck-Tafeln
Mortalität

Quelle